- June 22, 2023
Understanding Quantum Secrecy

We begin with describing the core problem of quantum communication: the encoding (and decoding) of information. We distinguish between the classical elementary unit of information (bit) and the quantum elementary unit of information (qubit).
We end with a description of the core problem of quantum secrecy: quantum key generation and distribution.
Table of Contents:
1. Quantum Information and Communication
1.1 Classical information (bits)
1.2 Quantum information (qubits)
1.3 Entropy
2. Quantum Computation
2.1 Quantum computers
2.2 Quantum cryptanalysis
3. Quantum Key Distribution (Quantum Cryptography)
3.1 Quantum Secrecy
3.2 Eavesdropping
4. Summary
References
1. Quantum Information and Communication
key names: Claude Shannon, Benjamin Schumacher
key terms: photons, bits, qubits, entropy, probability
Here we define the central problem of classical (Sha48) and quantum communication (Sch95): the encoding of information.
We define and distinguish classical information (bits) and quantum information (qubits). Both bits and qubits can be defined in abstract mathematical terms and in real physical terms. We focus on the physical definition.
1.1 Classical information (bits)
The central problem of classical communication (Sha48) is this: how all messages are encoded as sequences of bits (that are as short (compressed) as possible).
A bit is the elementary unit of classical information. In physical terms, a bit is a two-state system that can be prepared in one of two distinguishable states — yes or no, true or false, 0 or 1. For example, a classical (digital) computer switch transistors on and off.
All signals (messages) can be represented as bits (numbers, text, images, videos, etc.). Table 1 shows how numbers get encoded as bits. Notice, for example, that 3 bits (i.e. 3 two-state systems) are needed to encode one number between 0 and 7.
| 1-bit binary numbers | 2-bit binary numbers | 3-bit binary numbers | Decimal equivalent |
|---|---|---|---|
| 0 | 00 | 000 | 0 |
| 1 | 01 | 001 | 1 |
| 10 | 010 | 2 | |
| 11 | 011 | 3 | |
| 100 | 4 | ||
| 101 | 5 | ||
| 110 | 6 | ||
| 111 | 7 |
Tab. 1: Binary numbers and their decimal equivalents.
One bit can be encoded using two different polarizations of a photon. There are two forms of photon polarization: linear and circular. The two states (measurements) of linear polarization: vertical |V⟩ and horizontal |H⟩. The two states (measurements) of circular polarization: right |R⟩ and left |L⟩.
(Ben91) > [P]hotons were never meant to store information, but rather to transmit it.
We use photons as an example of a physical system that can represent bits (i.e. represent two states) because they are ideal candidates for transmitting information; after all, it’s how the universe does it.
1.2 Quantum information (qubits)
The central problem of quantum communication (Sch95) is this: how all messages are encoded as sequences of qubits.
(Nei01) > [Q]ubits, like bits, are realized as actual physical systems … qubits exist in Nature.
A qubit is the elementary unit of quantum information. In physical terms, a qubit is any quantum system with at least two discrete quantum states: |0⟩ and |1⟩. For example, the two different polarizations of a photon (as noted above) or two states of an electron orbiting a single atom (Nie01).
So far, it seems that there is no distinction between bits and qubits. The distinction is this: unlike a bit, a qubit can exist in a continuum (“superposition”) of states between |0⟩ and |1⟩ — until it is observed (measured). When a qubit is measured, it only ever gives `0` or `1` (bit) as the measurement result — probabilistically.
To say the same thing again: both 0 and 1 are present in the same qubit — until it is measured. At the point of measurement, either the result is 0, with a given probability, or the result is 1, with given probability; the two probabilities combined will always equal unity. In this way, a qubit is hybrid — both analog (continuous) and digital (discrete).
1.3 Entropy
(Sha48) > A physical system, or a mathematical model of a system, which produces such a sequence of symbols governed by a set of probabilities is known as a stochastic process. We may consider a discrete source, therefore, to be represented by a stochastic process.
A quick note on Shannon Entropy (Sha48). Entropy is a measure of the information gained from decoding a (qu)bit — or a sequence of (qu)bits. Once a (qu)bit is decoded, the more improbable the message (or sequence of messages) the more information is received. That is to say, the greater reduction in uncertainty of the message receiver.
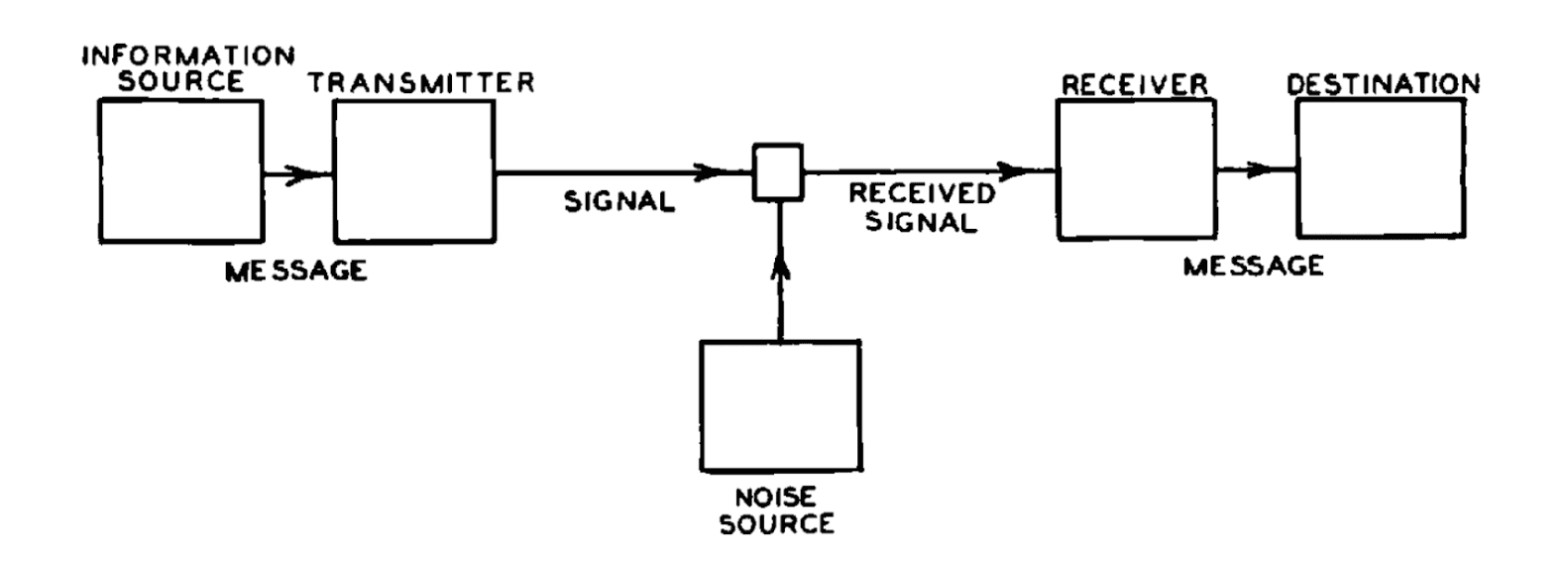
Fig. 1: Schematic diagram of a general communication system (Sha48). In quantum communication, the information source encodes a message as qubits. These qubits — e.g. photons — are transmitted to the receiver.
2. Quantum Computation
Now that we have a basic understanding of classical and quantum information, we can understand what the properties of quantum information enable quantum computers to do that classical computers cannot.
2.1 Quantum computers
A quantum computer performs operations on qubits. More specifically, quantum computers perform operations on the information encoded in qubits.
As noted above, a single qubit can exist in a superposition between its two discrete quantum states. Again, as an example, a photon can exist in a superposition of its linear polarizations: vertical |V⟩ and horizontal |H⟩.
However, we have not considered the entanglement between two or more qubits. For present purposes it is sufficient to accept as true that:

This is because the whole system of entangled qubits has a corresponding superposition. This ‘whole system superposition’ means that an entangled pair (or more) of qubits contains more information than each distinct qubit on their own.
To restate (1) but with a focus on quantum computation rather than quantum information:

For example, a 2-qubit computer can perform 4 operations, a 3-qubit computer can perform 8 operations, a 4-qubit computer can perform 16 operations, ad infinitum.
The core takeaway is this: to accomplish the same task as a quantum computer, a classical computer would have to repeat a computation 2N times — or 2N different processors would have to work in parallel.
2.2 Quantum cryptanalysis
What does the entanglement property of quantum computers mean for classical cryptography schemes?
A quantum computer running Grover’s Algorithm (Gro96, 97) can perform 2N search operations in one computational step. Some encryption standards simply require searching among possible keys. Quantum computers could search these possible keys far faster than classical computers.
(Gro97)> The search problem is this: there is an unsorted database containing N items out of which just one item satisfies a given condition - that one item has to be retrieved. Once an item is examined, it is possible to tell whether or not it satisfies the condition in one step.
A quantum computer running Shor’s Algorithm (Sho94) can perform 2N operations to factorize a number in one computational step. The security of RSA cryptography (Riv78) ultimately lies on the inability of classical computers to effectively factor large integers. A quantum computer running Shor’s Algorithm renders RSA insecure.
(Nie01) > [The Factoring Problem]: Given a positive composite integer N, what prime numbers when multiplied together equal it?
This consequence of quantum computers is why NIST began a competition to create a post-quantum cryptographic standard in 2016; to standardize quantum-resistant cryptographic algorithms.
3. Quantum Key Distribution (Quantum Cryptography)
key names: Charles H. Bennett
key terms: quantum key distribution, eavesdropping, Heisenberg Uncertainty Principle (HUP)
Post-quantum cryptography (or, quantum resistant cryptography) concerns the increased power of a cryptanalyst in breaking classical cryptography schemes. Quantum key distribution concerns the generation of cryptographic keys that protect information from an eavesdropper.
3.1 Quantum Secrecy
The central problem of classical cryptography (Sha49): how all messages (which are encoded as sequences of bits) can be encrypted (and decrypted) with a key (which is a sequence of bits) such that only the intended parties can decode the message.
(Sha49) > "Perfect Secrecy" is defined by requiring of a system that after a cryptogram is intercepted by the enemy the a posteriori probabilities of this cryptogram representing various messages be identically the same as the a priori probabilities of the same messages before the interception.
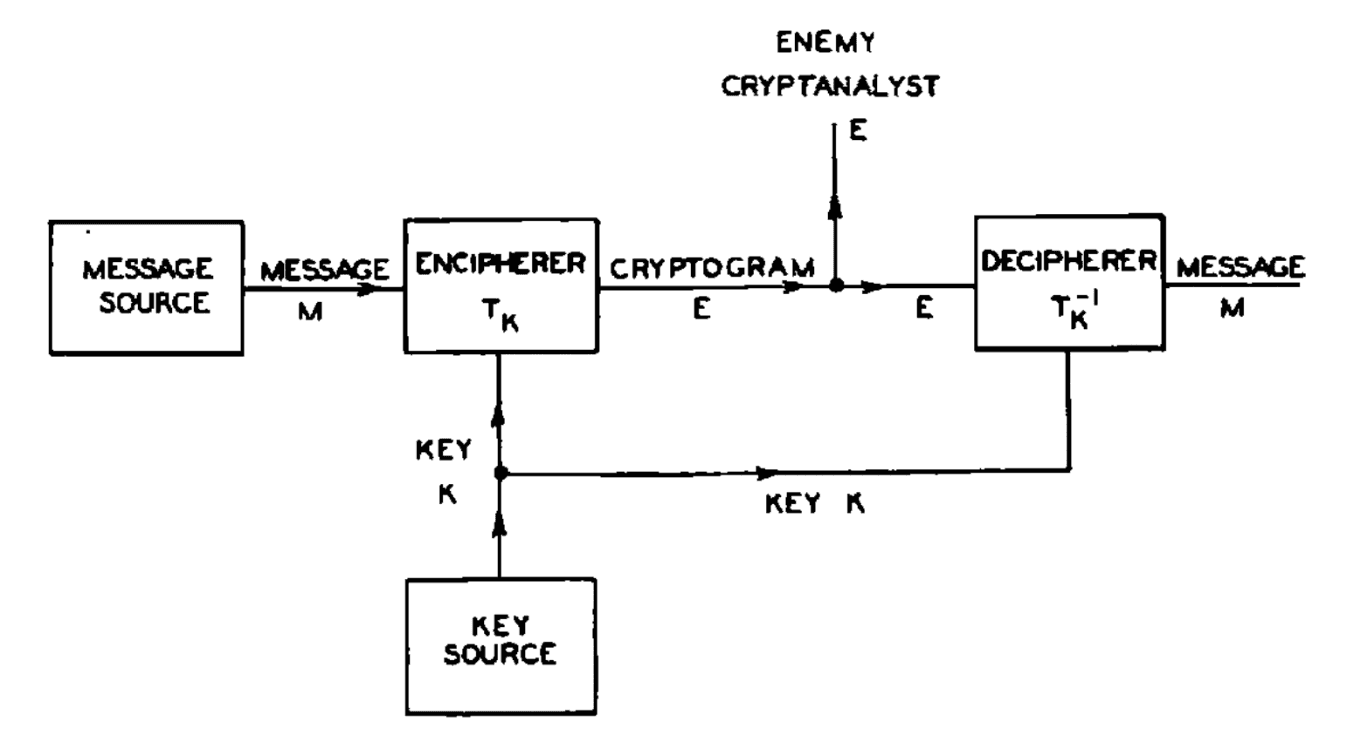
Fig. 2: Schematic diagram of a general secrecy system (Sha49).
Quantum key distribution (QKD) uses the properties of quantum information and communication for the generation of a classical key (i.e. a sequence of bits that is combined with the message bits).
As noted above, bits can be encoded using two different polarizations of a photon. There are two forms of photon polarization: linear and circular. The two states (measurements) of linear polarization: vertical |V⟩ and horizontal |H⟩. The two states (measurements) of circular polarization: right |R⟩ and left |L⟩.
The QKD scheme described in (Ben91) uses the two different polarizations of a photon to generate a key:
- Alice encodes and transmits a random sequence of photons that are each polarized: horizontal (↔), vertical (⭥), right-circular (↩︎) and left-circular (↪︎);
- Bob measures one of the properties of the photons' polarization — rectilinear (+) and circular (○) — in a random sequence. (Note: as described in 3.2, Bob can only measure one of the properties at one time due to the Heisenberg Uncertainty Principle);
- Results of Bob's measurements (some photons may not be received at all).
- Bob tells Alice which property he measured for each photon he received;
- Alice tells him which properties were correct;
- Alice and Bob keep only the data from these correctly-measured photons, discarding all the rest.
- This data is interpreted as a bit sequence according to the coding scheme ↔ = ↪︎ = 0 and ⭥ = ↩︎ = 1.
- The resulting bit sequence is a shared secret key between Alice and Bob that can be combined with message bit-sequences for their encryption and description.
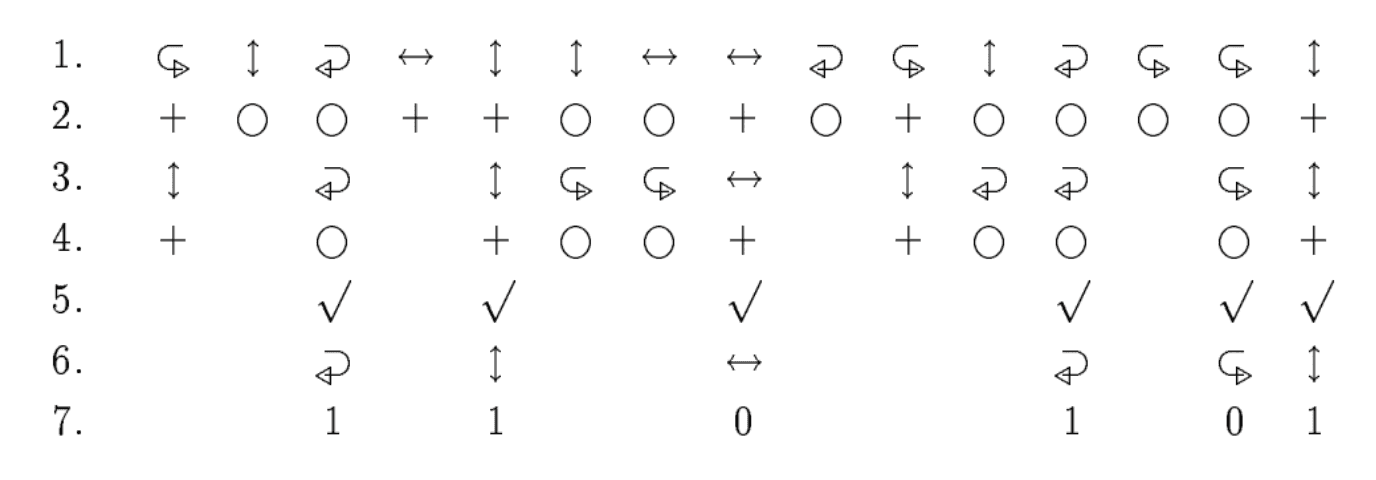
Fig. 3: Basic quantum key distribution protocol (Ben91).
For a visual animation of QKD, see Quantum Key Distribution Animation.
3.2 Eavesdropping
In the basic protocol, Alice and Bob test for eavesdropping on the transmission of the photons by publicly comparing polarizations of a random subset of the photons on which they think they should agree to use as the key bit sequence.
Any measurement of one of the photons by an eavesdropper, Eve, would have perturbed the photon.
The essential quantum property involved is the existence of pairs of properties that are incompatible in the sense that measuring one property necessarily randomizes the value of the other. For example, measuring a single photon's linear polarization randomizes its circular polarization, and vice versa.
Assuming Bob made the correct measurement on the photon in question — i.e. Bob measured the rectilinear (+) property of the photon which was the same as the property chosen by Alice when transmitting the photon — Alice and Bob can determine whether or not the photon has been perturbed. For example, if Alice encoded the photon with vertical (⭥) linear (+) polarization and Eve measured the circular (○) polarization of the photon, there is a chance (though not always) that Eve’s measurement perturbs the photon to have a horizontal (↔) linear (+) polarization. Alice and Bob would be able to notice this discrepancy as they interpret the sequence of photons (Step 6 as described in 3.1)
If the photons are not altered during transmission, Alice and Bob can be sure that Eve has not measured the values of those photons — and can proceed to use these photons in coding a key bit sequence.
(Ben91) > Because the system depends on the uncertainty principle of quantum physics, instead of usual mathematical assumptions such as the difficulty of factoring, it remains secure against an adversary with unlimited computing power.
In summary, QKD turns the limitation of the Heisenberg Uncertainty Principle (that a measurement perturbs the system) into a potentially useful process, in which the perturbation uncovers the presence of an eavesdropper.
4. Summary
- We briefly described quantum information and communication, distinguishing between bits and qubits.
- We showed that entangled qubits enable a quantum computer to perform 2N operations in one computational step, where N is the number of qubits. It is this property of quantum computation that makes classical cryptography schemes vulnerable — and why NIST is standardizing quantum-resistant cryptography schemes.
- We showed that quantum key distribution provides a method for parties to have full certainty as to whether a key was intercepted by an eavesdropper because all eavesdropping measurements perturb the quantum information (to some extent).
References
Here is an index of references used.
- (Sha48) Shannon, C.E., 1948. A mathematical theory of communication.
- (Sha49) Shannon, C.E., 1949. Communication theory of secrecy systems.
- (Riv78) R. L. Rivest, A. Shamir, L. Adleman., 1978 Public key cryptography
- (Deu85) Deutsch, D., 1985. Quantum theory, the Church–Turing principle and the universal quantum computer.
- (Ben92) Bennett, C.H., Bessette, F., Brassard, G., Salvail, L. and Smolin, J., 1992. Experimental Quantum Cryptography
- (Sho94) Shor, P.W., 1994, November. Algorithms for quantum computation: discrete logarithms and factoring.
- (Sch95) Schumacher, B., 1995. Quantum coding
- (Gro96) Grover, L.K., 1996, July. A fast quantum mechanical algorithm for database search.
- (Spi96) Spiller, T.P., 1996. Quantum information processing: cryptography, computation, and teleportation.
- (Gro97) Grover, L.K., 1997. Quantum mechanics helps in searching for a needle in a haystack.
- (Nie02) Nielsen, M.A. and Chuang, I., 2002. Quantum computation and quantum information.


