In December 2022, NIST announced that SHA-1 should be exhaustively phased out by Dec. 31, 2030 (after officially deprecating SHA-1 in 2011). In this post, we gain insight into the events leading to this (perhaps belated) announcement.

• First, we introduce the basic principles and use cases of hashing and give a brief description of SHA-1.
• Second, we introduce the basic principles of collisions and give a brief overview of the history of (theoretical and practical) SHA-1 collision attacks. We state the implications of SHA-1 collision attacks becoming practical — and use a hypothetical scenario in which Evervault Cages exclusively use SHA-1 (instead of SHA-384) to show how robust the cryptographic attestation is.
• We conclude with two recommendations; one conventional (to deprecate SHA-1 everywhere) and one less conventional.

1 Hashing

In 1.1, we define hashing. In 1.2, we provide a brief (technical) description of SHA-1.

1.1 Hashing

Key names: Claude Shannon

Key terms: hash function, hash algorithm, hashing, digital signatures, message authentication, password hashing, content-addressable storage, SHA-1, SHA-256

Cryptographic hash functions are primitives used in many applications, including:

1. digital signature schemes,
2. message authentication codes,
3. password hashing, and
4. content-addressable storage.

Informally, a hash function H is a function that takes an arbitrarily long message M as input and outputs a fixed-length hash value of size n bits.

The particular output depends on the specific hash function being used — such as SHA-1 or SHA-256. However, a given hash function always returns the same value for a given input.

Let’s take two example inputs:

Input string 1: Claude Shannon
Input string 2: Ralph Merkle

Side note: In our example, we input strings into the hash function, and not the underlying byte sequences those strings actually represent. If we insert this string directly into the hash function, programming languages may actually send the ASCII encoding of each of the characters into the hash function. What we actually want to send into the hash function is the byte this hexadecimal string represents. Most programming languages will have functions that allow you to convert hexadecimal strings into bytes first before hashing. All data is essentially bytes.

Every time that we run these inputs through the SHA-1, SHA-256 and SHA-384 functions, we should always get:

Table 1: Example outputs of SHA-1, SHA-256 and SHA-384. We include SHA-384 for its relevance in relation to our discussion of Evervault Cages in 2.3.

The SHA-256 hash is longer than the SHA-1 hash because SHA-1 creates a 160-bit hash, while SHA-256 creates a 256-bit hash.

Here is a table of SHA properties:

Table 2: Properties of SHA-1, SHA-256, and SHA-384 hash functions. We include SHA-384 for its relevance in relation to our discussion of Evervault Cages in 2.3. The meaning of block and word will become clearer in 1.2. After FIPS PUB 180-4.

In theory, a hash function could accept as the message M a file or even an entire file system. Of course, the computation time and power needed to obtain the hash would become impractical at certain message sizes.

To end this section, let’s list the characteristics (or design principles) of hash functions:

1. Deterministic -- a given hash algorithm always returns the same value for a given input;
2. **Unique **-- it’s computationally infeasible to generate the same hash output from two different inputs; and
3. One-way -- it’s computationally infeasible to compute the input from its hash.

These characteristics are relevant to our discussion of collision and preimage resistance are discussed in 2.

1.2 Technical description of SHA-1

Key names: Ralph Merkle, Ivan Damgård

Key terms: Merkle-Damgård construction, compression function, MD-SHA family, Davies-Meyer construction, word, block, padding, partitioning, processing

Now we have a basic understanding of hash functions, let us provide ourselves with a (brief) more technical description of how the SHA-1 hash function works. It follows the Merkle-Damgård construction.

1. Padding: Different inputs to SHA-1 are different lengths (up to the limit 2⁶⁴). The input should be considered to be a bit string. The length of the message is the number of bits in the message. (An empty message has length 0.) SHA-1 sequentially processes blocks of 512 bits when computing the input. Therefore, if the length of the input is not a multiple of 512, it needs to be padded to make it so.
2. Partitioning: Once padded to have a length with a multiple of 512 bits, the padded input is then partitioned by the SHA-1 as N 512-bit blocks.
3. Processing: To hash the padded input consisting of N partitioned blocks, SHA-1 goes through N+1 states called intermediated hash values. Each intermediate hash value is computed using the SHA-1 compression function. For a description of the SHA-1 compression function see FIPS 180–1: Secure Hash Standard.
4. Output: The resulting hash value is the last intermediate hash value (IHV_N), i.e. the final chaining value. This output is a 160-bit string (as noted in 1).

2 Collisions

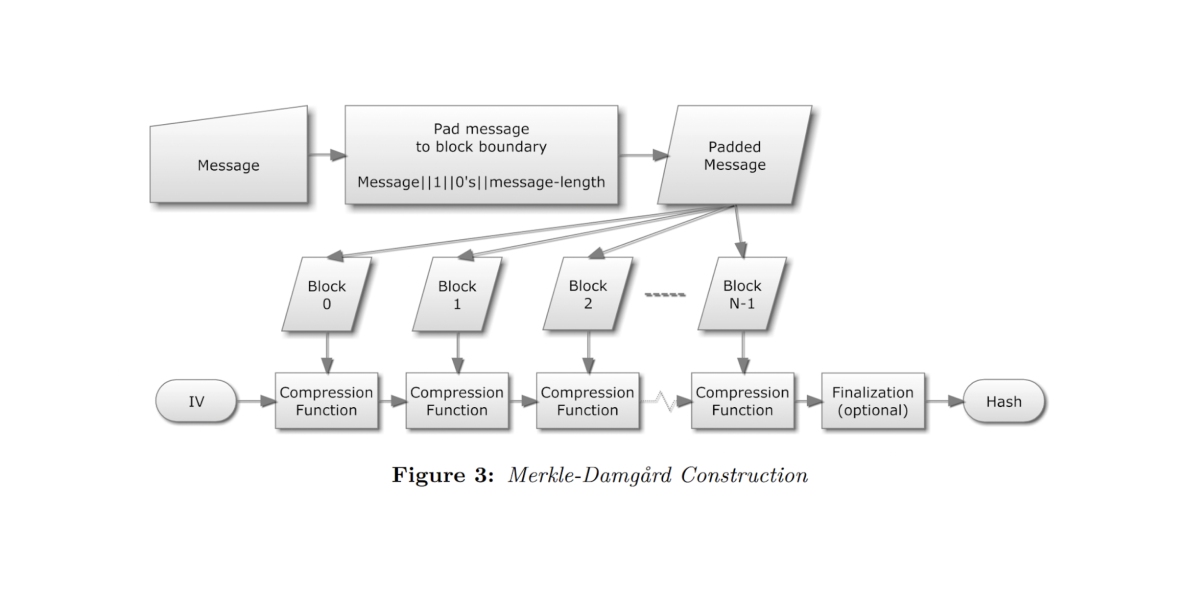
In 2.1, we define collision resistance, preimage resistance, and second preimage resistance. In 2.2, we look at the history of collision attacks on SHA-1. In 2.3, we consider the implications of this history with a hypothetical example related to Evervault Cages.

2.1 Collisions and preimages

Key terms: cryptanalysis, collisions, collision resistance, brute force, preimage resistance, collision attacks

Key names: Xiaoyun Wang, Marc Stevens, Gaëtan Leurent, Thomas Peyrin

There are three forms of resistance that hash functions must satisfy: collision resistance, preimage resistance and second preimage resistance. Let’s define these — and give the expected security strength of a hash function in relation to each form.

2.1.a Collision resistance

Informally, we can define collision resistance: It is computationally infeasible to find two different inputs to the hash function that have the same hash output. That is, a collision is two different inputs M₁ and M₂ for which H(M₁) = H(M₂).

To continue with our examples from 1, a collision is the first input Claude Shannon and the second input Ralph Merkle having the same output.

Collision resistance is measured by the amount of work that would be needed to find a collision for a hash function with high probability. If the amount of work is 2N , then the collision resistance is N bits. The expected collision-resistance strength of a hash function is half the length of the hash value produced by that hash function, i.e. for a hash function with an n-bit output, this requires about 2^n/2 steps.

For example, SHA-1 produces a (full-length) hash output of 160 bits (see Table 1). Therefore, SHA-1 provides an expected collision resistance of 80 bits, i.e. 2⁸⁰.

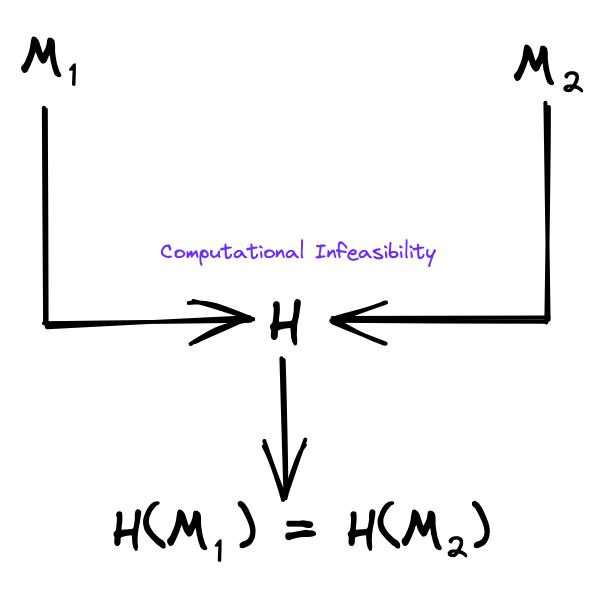
Figure 3: Collision resistance.

2.1.b Preimage resistance

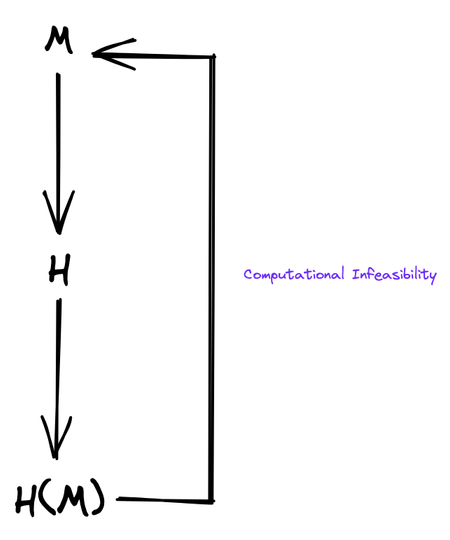
Informally, we can define preimage resistance: Given a randomly chosen hash output X, it is computationally infeasible to find an input M so that H(M) = X. This property is also called the one-way property (as noted in 1.1).

To continue with our examples from 1, if we were given the SHA-1 output 910aa6b1c4c160e1529161ac6006968fd3f0ff21, it should be infeasible for us to compute the input Claude Shannon. Equally, if we were given the SHA-1 output 56736dcbba157b150cf0d953ee0689d9645acf8a, it should be infeasible for us to compute the input Ralph Merkle.

Preimage resistance is measured by the amount of work that would be needed to find a preimage for a hash function with high probability. If the amount of work is 2N , then the preimage resistance is N bits. The expected preimage-resistance strength of a hash function is the length of the hash output produced by that hash function, i.e. for an n-bit hash function, the expected security strength for preimage resistance is n bits. The generic preimage attack requires about 2ⁿ steps.

For example, SHA-1 produces a (full-length) hash value of 160 bits. Therefore, SHA-1 provides an expected preimage resistance of 160 bits.

2.1.c Second preimage resistance

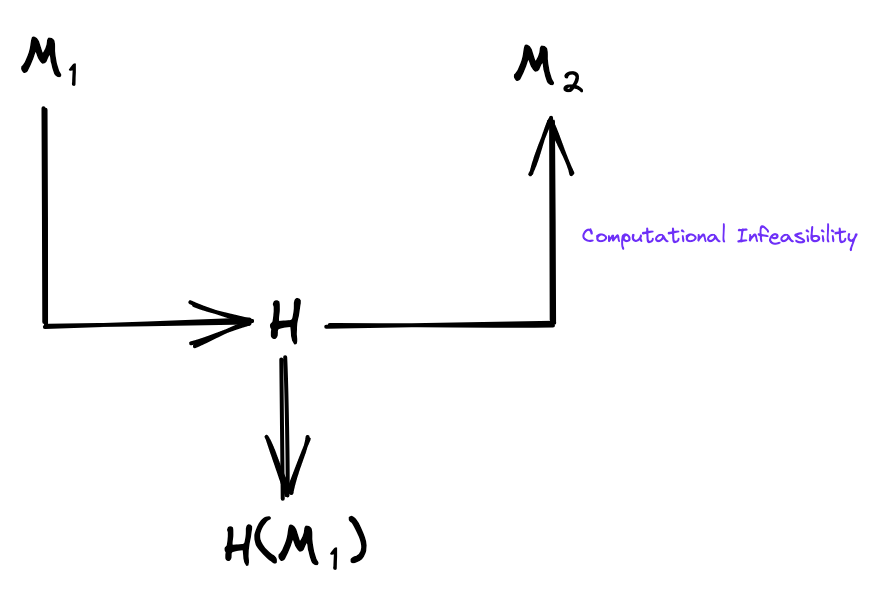
Informally, we can define second preimage resistance: It is computationally infeasible to find a second input that has the same hash value as any other specified input. That is, given an input M₁, it is computationally infeasible to find a second input M₂ that is different from M₁, such that H(M₁) = H(M₂).

To continue with our examples from 1, if we were given the hash input Claude Shannon, it should be infeasible for us to compute a second hash input that has the same hash output 910aa6b1c4c160e1529161ac6006968fd3f0ff21.

Second preimage resistance is measured by the amount of work that would be needed to have a high probability of finding a second preimage for a hash function. If the amount of work is 2N , then the second preimage resistance is N bits. In general, the expected second preimage strength of a hash function is the length of the hash value produced by that hash function, i.e. for an n-bit hash function, the expected security strength for second preimage resistance is n bits. The generic second preimage attack requires about 2ⁿ steps.

For example, SHA-1 produces a (full-length) hash value of 160 bits. Therefore, SHA-1 provides an expected second preimage resistance of 160 bits.

Table 3: Expected security strength of SHA-1, SHA-256 and SHA-384. Again, security strength is a number associated with the amount of work (that is, the number of hash operations) that is required to break a hash function. If 2N execution operations of the function are required to break it, then the security strength is N bits. After NIST Special Publication 800-107.

For the remainder of this post, we focus on collision resistance because, as we will see, the current state of cryptanalysis against SHA-1 allows for collisions that are faster than a generic search (which, as we will see next, is the definition of “breaking” a function), but not for preimages.

2.1.d Broken functions

What does it mean for a hash function to be broken by a collision? A hash function is called broken when there exists a known explicit attack that is faster than the general brute force attack for a security property (i.e. for collisions or preimages). This requires a definition of brute force attack — and of the known explicit attacks that are faster with respect to SHA-1.

• Brute-force search (generic attack): An attack in which hashes H(M_n) are computed for randomly chosen inputs M_n until an input M₂ is found where H(M₁) = H(M₂) — and M₂ ≠ M₁.
• Identical-prefix collisions: An attack which takes a prefix P and finds two message blocks (m₁)≠(m₂) such that for any suffix s: H(P ‖ m₁ ‖ s)= H(P ‖ m₂ ‖ s), where || denotes concatenation.

• Chosen-prefix collisions: An attack which takes two given input prefixes P₁ ≠ P₂ and finds middle blocks m₁ ≠ m₂ such that for any suffix s: H(P₁ ‖ m₁ ‖ s ) = H(P₂ ‖ m₂ ‖ s) , where || denotes concatenation.

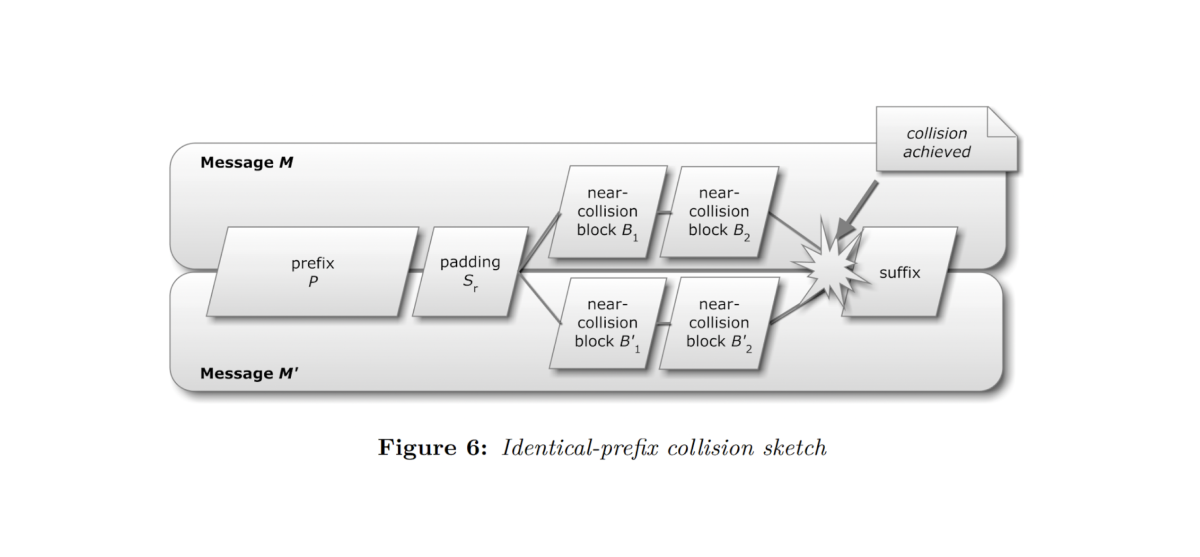
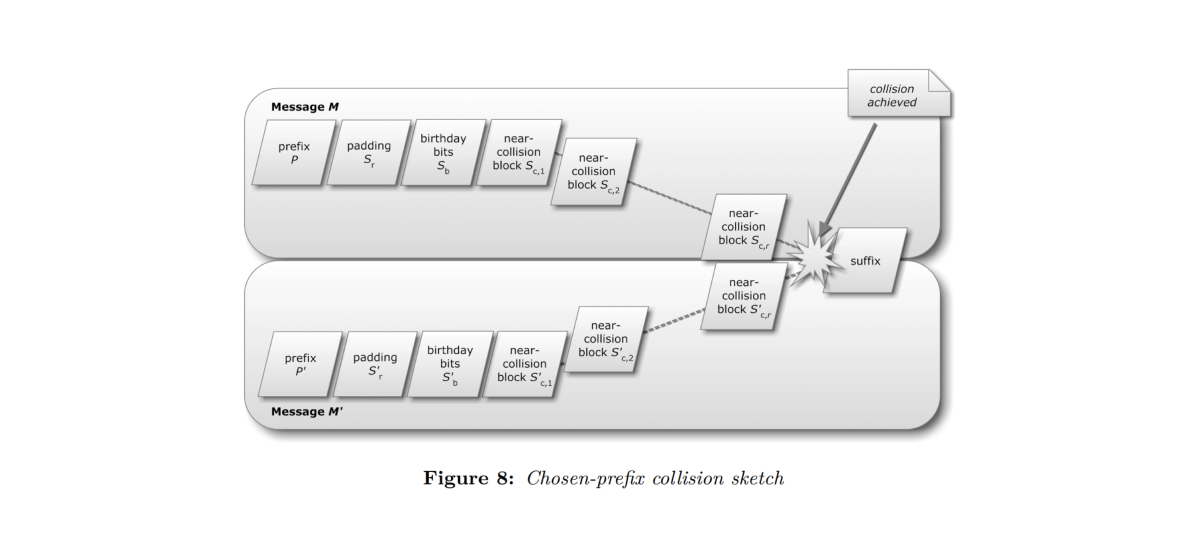
Figure 7: Chosen-prefix collision. Near-collision denotes one “hash operation”. After (Ste12).

For a complete description of collision attacks, we recommend Marc Stevens’ thesis: Attacks on hash functions and applications (from which the above definitions and figures are derived).

2.2 History of SHA-1 collision attacks

Key names: Satoshi Nakamoto

Key terms: SHAttered, SHAmbles, hash operations, computational complexity, GPU, PS3, PlayStation 3, Bitcoin, hashrate, mining

Now we have a basic understanding of collisions and collision attacks, let us look at the history of SHA-1 collision attacks. It is this history of SHA-1 collision attacks that led to NIST announcing in December 2022 that SHA-1 should be phased out by Dec. 31, 2030.

Before listing the events, given our discussion in 2.1, we can establish that the main question to be asked in relation to collision attacks is related to computational complexity: how many hash operations must be performed before a collision is found?

• 2005: [Wan05] found theoretical collisions of SHA-1 can be found with complexity less than 2⁶⁹ SHA-1 hash operations.
• 2013: [Ste13] presented a theoretical identical-prefix collision attack and a chosen-prefix collision attack on SHA-1 with complexities equivalent to approximately 2⁶¹ and 2^77.1 SHA-1 hash operations, respectively.
• 2015: [Ste16] presented a practical GPU implementation of a freestart colliding pair for SHA-1 (i.e. a collision for its internal compression function) with a runtime cost equivalent to approximately 2^57.5 hash operations.
• 2017: [Ste17] presented a practical GPU implementation of [Ste13]. The total computational effort spent was equivalent to 2^63.1 hash operations, and took approximately 6,500 CPU years and 100 GPU years.

• 2019: [Leu19] presented a theoretical chosen-prefix collision with a conservative hypothesis of a complexity of 2^67.7 hash operations.
• 2020: [Leu20] presented practical GPU implementation of identical-prefix collisions computed with a complexity of 2^61.2 hash operations and chosen-prefix collisions with a complexity of 2^63.4 hash operations. The chosen-prefix collision attack took approximately 107 GPU years and cost about US$45k.

All these attacks have exceeded the expected SHA-1 collision resistance of 2⁸⁰ — and this history of collision attacks on SHA-1 shows definitively that theoretical attacks have now become practical. With other words, the compute time and energy (power) needed to obtain a collision faster than a brute force search (the definition of a hash function being broken) is trending downwards such that a successful collision attack could be performed in the real world — on a cloud GPU, or even a PS3:

We can infer from this history of SHA-1 collision attacks that if the hash function used in the mining of Bitcoin block hashes was SHA-1, the difficulty level would be too low for the security of the protocol.

Equivalently, if instead of miners competing to find a SHA-256 block hash below the current target, miners aimed to compute SHA-1 collisions, we could determine from the total hashrate of the Bitcoin protocol how many collisions the miner network would compute for any given time interval.

(Note: Bitcoin uses the HashCash proof-of-work scheme which employs partial hash collisions.)

Of course, at the time of writing, the main hash function used in Bitcoin is SHA-256, so this vulnerability is not an immediate concern (assuming SHA-256 is unbroken).

The general point: the tactics and learning from practical implementation of collision searches (brute force, or otherwise) can be applied to Bitcoin block hash searches — and vice versa.

To end this section, we note that our focus was the complexity of computing a collision for SHA-1 and not the actual implementation of the collision attacks. You can read more about the 2017 implementation here (SHAttered) and the 2020 implementation here (SHAmbles).

2.3 Evervault Cages

Before we conclude this post, let’s have a brief look at a hypothetical scenario for Evervault Cages. If you are unfamiliar with Evervault Cages, it’s worth watching our overview (or reading our docs) before reading this section.

Let’s assume that Evervault Cages (and AWS Nitro Enclaves) use exclusively SHA-1 (and not SHA-384 (which is part of the SHA-2 family of hash functions)), and let’s ask the question: What is the probability that two Cage Images could collide such that a “malicious” Cage Image could pass attestation?

The primary function of the attestation process is to guarantee to the developer that the code running in the Cage is the image written by the developer locally. In theory, it is possible that an alternative Cage Image (“bad image”) collides with the developer’s Cage Image (“good image”). In practice, however, AWS Nitro Enclaves have been designed such that the probability of colliding images converges to zero.

Even if we assume that the attacker has knowledge of (a) the hash function (again, we assume Cages exclusively uses SHA-1 instead of SHA-384), and (b) the specific Evervault API key related to the “good” Cage Image in question, the probability of colliding hashes for **all **PCRs (the measurements used to attest the Cage) — such that attestation is passed — is practically zero.

Evervault Cages — and the AWS Nitro Enclaves underlying them — are designed such that if one PCR is invalid, attestation fails. Not only would the attacker need to collide a hash of the “bad” Cage Image with that of the “good” Cage Image — but a hash of the parent instance ID and a hash of the ARN of the attached AWS IAM role, as well. (The attacker would not necessarily need to create a collision for these latter two hashes, but simply have the respective valid hash.)

To end this section, here are example SHA-384 PCRs — let us know at shattered@evervault.com if you can perform a preimage attack on any of them.

1[attestation]
2HashAlgorithm = "Sha384 { ... }"
3PCR0="8576aa759528d6dc82b6a35504edf491bcf245266acb5745f7f15801e15988a5abbc8c637af3edeb96efcbe8e8a433a1"
4PCR1="bcdf05fefccaa8e55bf2c8d6dee9e79bbff31e34bf28a99aa19e6b29c37ee80b214a414b7607236edf26fcb78654e63f"
5PCR2="4ffe3d8b0211341c9eac73abccfcfed63f694a4a84b7758e70d1941d0ac6c0a7091c7860aa1ff2e4d39bbdd2b220608f"
6PCR8="9f357c7861268d124143701d30fbd0401f4f2854db7698851c51a08bc719abe9cc89645324d24cdbac1f216b482d6ad8"

Conclusion

Key terms: SHA-1 deprecation, BLAKE2, unbroken hash functions

The implication of SHA-1 collisions being practical (not simply theoretical) is that if any of the four example application types from 1 (digital signature schemes, message authentication co des, password hashing, and content-addressable storage) were using SHA-1, they would all be vulnerable to attackers who could obtain colliding signatures, codes, passwords, or files respectively. However, since SHA-1 usage has significantly decreased in the last few years (especially since 2017), it may seem that this post is somewhat redundant. However, as time goes on all hash functions may become vulnerable to collision attacks — not only SHA-1. Therefore, as computational time decreases and power increases, the analyses and principles described above are relevant to hash functions that are (at the time of writing) considered more secure.

In any case, we close by saying: remove any use of SHA-1 in your products as soon as possible and instead use SHA-256 or SHA-3 (KECCAK) — or alternatives, like BLAKE2.

If NIST is phasing out SHA-1 by Dec. 31, 2030, perhaps SHA-2 (that’s SHA-2) should be phased out from your products by then, too. Of course, when it comes to cryptography, it’s always good to be ahead of the curve.

Further reading

Here we provide four further readings; one theoretical (and historical), three practical.

Theoretical

Key terms: one-way hash function, Merkle Hash Trees, binary trees, Merkle Trees

If you’re curious about the theoretical origin of (one-way) hash functions for digital signature schemes, there’s no better place to start than Ralph Merkle’s 1979 Thesis: Secrecy, Authentication, And Public Key Systems.

Practical

Key terms: BLAKE3, KECCAK, sponge construction, sponge function, Ascon, lightweight cryptography

1. If you’re curious about the piece-by-piece implementation of hashing algorithms consider The SHA-256 Project by @oconnor663, one of the designers of BLAKE3.
2. If you want to know more about SHA-3 — the most current NIST standard — FIPS PUB 202 is where to start. SHA-3 is based on KECCAK, which is a sponge construction.
   A sponge construction is a method for defining a hash function from the following: (a) an underlying function on bit strings of a fixed length, (b) a padding rule (see 1.2 above), and 3) a rate (i.e. the number of input bits processed or output bits generated per invocation of the underlying function). Both the input and the output of the resulting function are bit strings that can be arbitrarily long. For more information about sponge constructions, see Cryptographic Sponge Functions.
3. By 2025, there may be more than 75 billion Internet of Things (IoT) connected devices in use. Many IoT sensor nodes are resource-constrained, demanding low computation and memory consumption. Therefore, NIST initiated a competition to select a standard for Lightweight Cryptography (LWC) — including hash functions — with applications to resource-constrained systems. In February 2023, NIST announced that the Ascon family (which adopts the sponge construction) will be standardized. Since Ascon is targeting lightweight applications, its designers do not claim resistance against all possible quantum attacks. However, Ascon provides enough robustness and agility to provide basic resistance against certain classes of attacks (once the availability of appropriate quantum computer resources becomes evident).

References

Most references are linked within the post. Here we reference only the main resources used. [Wan05] Wang, X., Yin, Y.L. and Yu, H., 2005. Finding collisions in the full SHA-1

[Ste13] Stevens, M., 2013. New collision attacks on SHA-1 based on optimal joint local-collision analysis

[Ste16] Stevens, M., Karpman, P. and Peyrin, T., 2016. Freestart collision for full SHA-1

[Ste17] Stevens, M., Bursztein, E., Karpman, P., Albertini, A. and Markov, Y., 2017. The first collision for full SHA-1

[Leu19] Leurent, G. and Peyrin, T., 2019. From collisions to chosen-prefix collisions application to full SHA-1

[Leu20] Leurent, G. and Peyrin, T., 2020, August. SHA-1 is a shambles: First chosen-prefix collision on SHA-1 and application to the PGP web of trust

[Fer10] Ferguson, N., Schneier, B. and Kohno, T., 2011. Cryptography engineering: design principles and practical applications. John Wiley & Sons

[Ste12] Stevens, M., 2012. Attacks on hash functions and applications. Leiden University.