Engineer
I was initially planning to write an explanation of how the Advanced Encryption Standard (AES) works. However, to understand the design decisions for an encryption scheme, one must first understand which attacks it is trying to prevent. Of all the attacks AES is designed against, I find Differential Cryptanalysis (DC) the most interesting.
In this post, I will tell you how DC works, how it was used to disgrace IBM and the NSA, how we don’t know who truly discovered it, and how AES prevents it.
In 1973, the National Bureau of Standards (NBS, now known as NIST) made a request to the public for a new encryption standard. IBM submitted a proposal based on a previous algorithm named Lucifer (red flag). NIST chose IBM’s algorithm, and named it the Data Encryption Standard (DES). A key aspect of DES was the use of Substitution Boxes (S-Boxes), which are simple functions that take in an input and map it to a deterministic output. The DES S-Boxes take in inputs of 6 bits (six 1s and 0s) and output 4 bits (four 1s and 0s). Some of these mappings are shown below.
These mappings can be shown in a table, a.k.a. a Substitution Box. Here’s the table representing S-Box 1, one of the substitution boxes used in DES.
Don’t worry if you can’t immediately see how that table represents input-output mappings. In DES, the S-Box tables are quite inconvenient to use. It is somewhat tricky to find which row and column correspond to each input. It works by interpreting the outermost bits of the input as the row number (in binary), and the remaining bits as the column number. The following animation should help visualise it.
So, the input 110101 corresponds to Row 3, Column 10, which in the table is the value 3 (0011 in binary).
How were these mappings chosen? During IBM’s application to NIST, they were told to first seek approval of their algorithm from the National Security Agency (NSA). The NSA’s analysis was that they would approve the proposal, but only if IBM used S-Boxes the NSA created (they also convinced IBM to reduce the size of the secret keys used, but that’s a story for another day…). IBM agreed to these conditions.
Eight such S-Boxes (chosen by the NSA) were used in DES. The original DES standard from 1977 (which was a bit tricky to find) stated:
The choice of the primitive functions… is critical to the strength of an encipherment resulting from the algorithm.
Yet it didn’t state why the mappings in those S-Boxes were chosen. Or, more specifically, why the NSA had chosen them.
The academic cryptography community could not accept that a standard that contained arbitrary numbers hand-picked by the NSA should be set in stone. They suspected that the NSA could have given themselves a backdoor to allow them to decrypt data, so it became the academics’ mission to crack DES – and hopefully find this backdoor.
One of the most in-depth analyses, titled “Results Of An Initial Attempt To Cryptanalyze The NBS Data Encryption Standard”, was published by Whitfield Diffie and Martin Hellman, of the Diffie-Hellman Key Exchange. I’d recommend skimming this paper, because watching them go after IBM and the NSA so viciously is a reminder that academic writing wasn’t always so boring. Plus, reading cryptography papers in that font makes you feel like you’re a spy who has been rifling through filing cabinets.
DES remained a target for academia for many years. In 1991,Adi Shamir, famous for RSA and Shamir’s Secret Sharing, used DES as the unfortunate victim in the grand reveal of his latest weapon: Differential Cryptanalysis.
Typically cryptanalysis involves analyzing ciphertexts (values after encryption) and perhaps comparing them to their plaintexts (values before encryption). In DC, the differences between two plaintexts and the differences between their corresponding ciphertexts are analyzed, as shown below.
So, we are using the analysis of differences to break cryptography schemes, hence the term Differential Cryptanalysis. The difference between two binary values is typically calculated using an exclusive-or (XOR) operation. Basically you compare corresponding bits in each sequence. If the bits are equal, record a zero. If the bits are different, record a 1. The symbol for XOR is ⊕.
To analyze an S-Box using this method, we observe the difference between two inputs before entry to the S-Box and then observe the difference between the outputs. Here’s an example of taking two sample inputs to DES’s S-Box 1 and observing the input and output differences.
To fully analyze the S-Box, Shamir took all possible pairs of plaintexts, and created a table counting how many times a particular input difference would result in a particular output difference. Here’s a complete description of his experiment:
This results in a table that counts how often an input XOR will produce a specific output XOR. The hope of the cryptanalyst is that this table will show interesting relationships between input differences and output differences, e.g. if one knows the output XOR of two values, can one estimate the most likely input XOR to create such a result? This table is called a differential distribution table (DDT).
When we run this experiment on S-Box 1, we find that the counts are not evenly distributed. For example, consider the row corresponding to the input XOR 110100 (0x34 in hex). It is shown below in heatmap form, where the “hottest” values have the highest counts for emphasis.
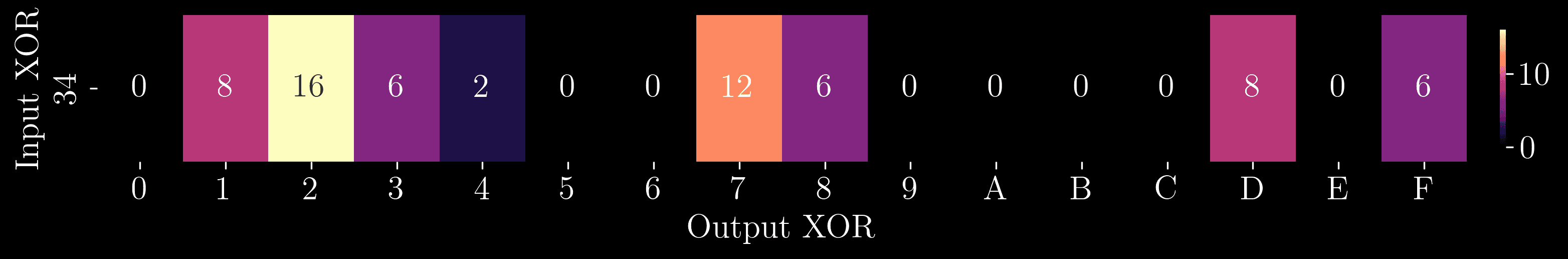
We can see that the counts are not evenly distributed across the columns. For the 64 pairs of inputs with an input XOR of 0x34, 16 result in an output XOR of 0x2 (0010 in binary). Hence, an input XOR of 0x34 results in an output XOR of 0x2 with probability 25% (16/64). Many rows in the S-Box 1 DDT have similar uneven distributions. The full heatmap of the table is shown below.
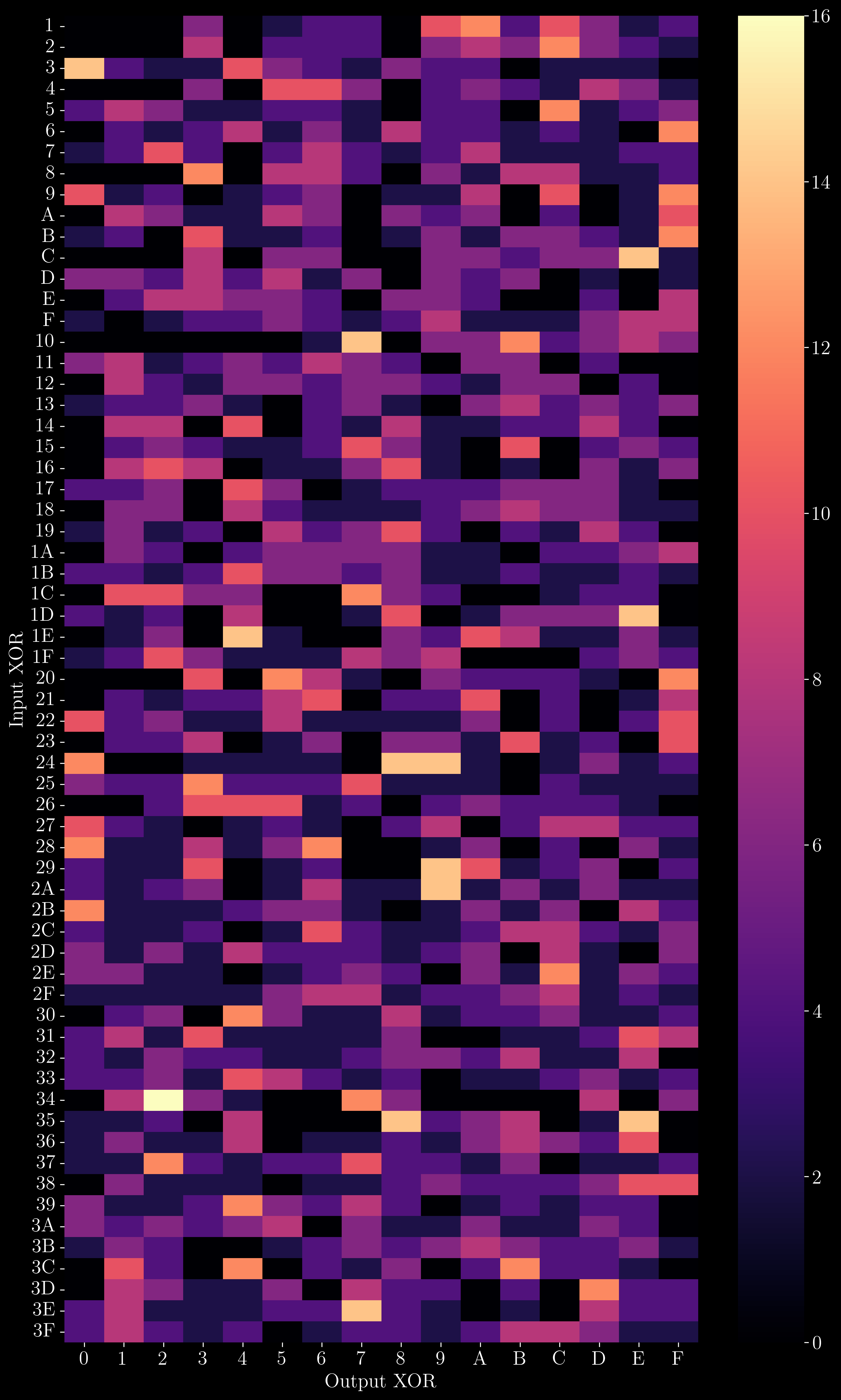
How do you use these DDTs to find secret keys? It depends on the algorithm you’re trying to break. Usually, the ability to perform a “chosen plaintext attack” is needed. In a chosen plaintext attack, you have the ability to choose which plaintexts get encrypted, and view the resulting ciphertexts. This allows you to calculate what the input difference and output difference was. You would then try to track how differences propagate through the algorithm, using the DDT to find out which secret keys are most probable/possible to have resulted in the output differences you found.
To demonstrate the essence of how these differences can propagate through algorithms, the example below shows how the addition of a secret key via XOR (a common step in encryption algorithms) does not change the difference between two values.
Cryptanalysts need to analyse how each step in the algorithm they’re trying to crack will propagate these differences. DES is a complex, ugly algorithm (shown in the images below), which makes tracing these differences very verbose. Hence, I don’t think it’s worth including in this post. If you want the details, I refer you to Shamir’s paper.
Shamir’s paper came out in 1991. Three years later, it was revealed that IBM and the NSA had already been aware of DC since 1974. Apparently, the NSA S-Boxes included changes to prevent DC. Considering DES was still cracked using DC, it must have been much more vulnerable before the NSA made their alterations.
So, if the NSA knew about differential cryptanalysis, why didn’t they make it public? The NSA claim it was to “protect” existing schemes from being subject to DC. The skeptic would claim it was to allow the NSA to use DC to break ciphers while no one else could. I’ll let you pick your side on that one.
Nevertheless, we are still left with the question of who really invented DC. It seems to be like many other cases in history where the same discovery was made in multiple places around the same time. Could it have been the result of espionage? Could spies have told Shamir what the NSA had discovered? If I had to bet myself, I would guess that Shamir did discover it on his own accord. Innovation in science tends to involve a sequence of stepping stone discoveries before the treasure is found. I believe that the NSA and Shamir both had the same foundation of research stepping stones behind them, which allowed both to independently recognise that the next stone was DC.
In 1993, a Finnish cryptographer named Kaisa Nyberg made it her mission to figure out how to make S-Boxes that result in evenly distributed DDTs, releasing a paper titled “Differentially uniform mappings for cryptography”. She defined a measure of S-Boxes being “N-uniform”, where N is the highest count in the DDT. If you take another look at S-Box 1’s distribution table, you will see that it is 16-uniform, as the highest count is 16. Nyberg showed that having high numbers, such as 16, in the distribution table makes it easier for cryptanalysts to make predictions. Hence, a good S-Box has a low n-uniformity.
Nyberg gave examples of mathematical operations that could be performed on the input, such that the resultant outputs would form an S-Box of a deterministic number N. One of these was a proof that for a Galois Field with 2^n elements, the multiplicative inverse is a mapping that results in an S-Box, which is 4-uniform. I’ll show what that means next!
The AES scheme, which eventually replaced DES, also uses an S-Box as a step in its encryption rounds. AES’s S-Box takes in 8-bit inputs and produces 8-bit outputs. Under the hood, these 8-bit values are treated as polynomials. For example, here’s how the value 01100101 is represented as a polynomial:
The set of all 8-bit polynomials is the “field” that AES operates in, which has 2^8 elements. To make it a “Galois Field”, we need to be able to add and multiply elements, while ensuring that the result stays within the field. The next animation shows how to perform multiplication while ensuring that the result is always an 8-bit polynomial.
Addition is defined as regular polynomial addition followed by the “Coefficients modulo 2” step shown in the animation. So now we have a Galois Field containing 2^8 elements, which can be denoted as GF(2^8).
Nyberg proved that the multiplicative inverse mapping results in a 4-uniform S-Box. The multiplicative inverse of an element A is the element B such that A times B equals 1. For example, the polynomial 11001010 is the multiplicative inverse of the polynomial 01010011. We’ll use the same multiplication steps shown above to verify this:
As the result is 1, we’ve verified our claim by showing that 01010011 times 11001010 equals 1. To algorithmically find the multiplicative inverse of an element in the field, the Extended Euclidian Algorithm can be used. Finally, here is how the AES S-Box is constructed:
The first step is to convert an element into its multiplicative inverse, which is what Nyberg proved would result in a 4-uniform S-Box. Thankfully, the Affine Transformation step (which isn’t particularly relevant to this post), doesn’t affect the n-uniformity. If we run Shamir’s experiment on the AES S-Box, like we did on S-Box 1, we should expect it to have a maximum count of 4. Here’s the heatmap of the AES S-Box distribution table:
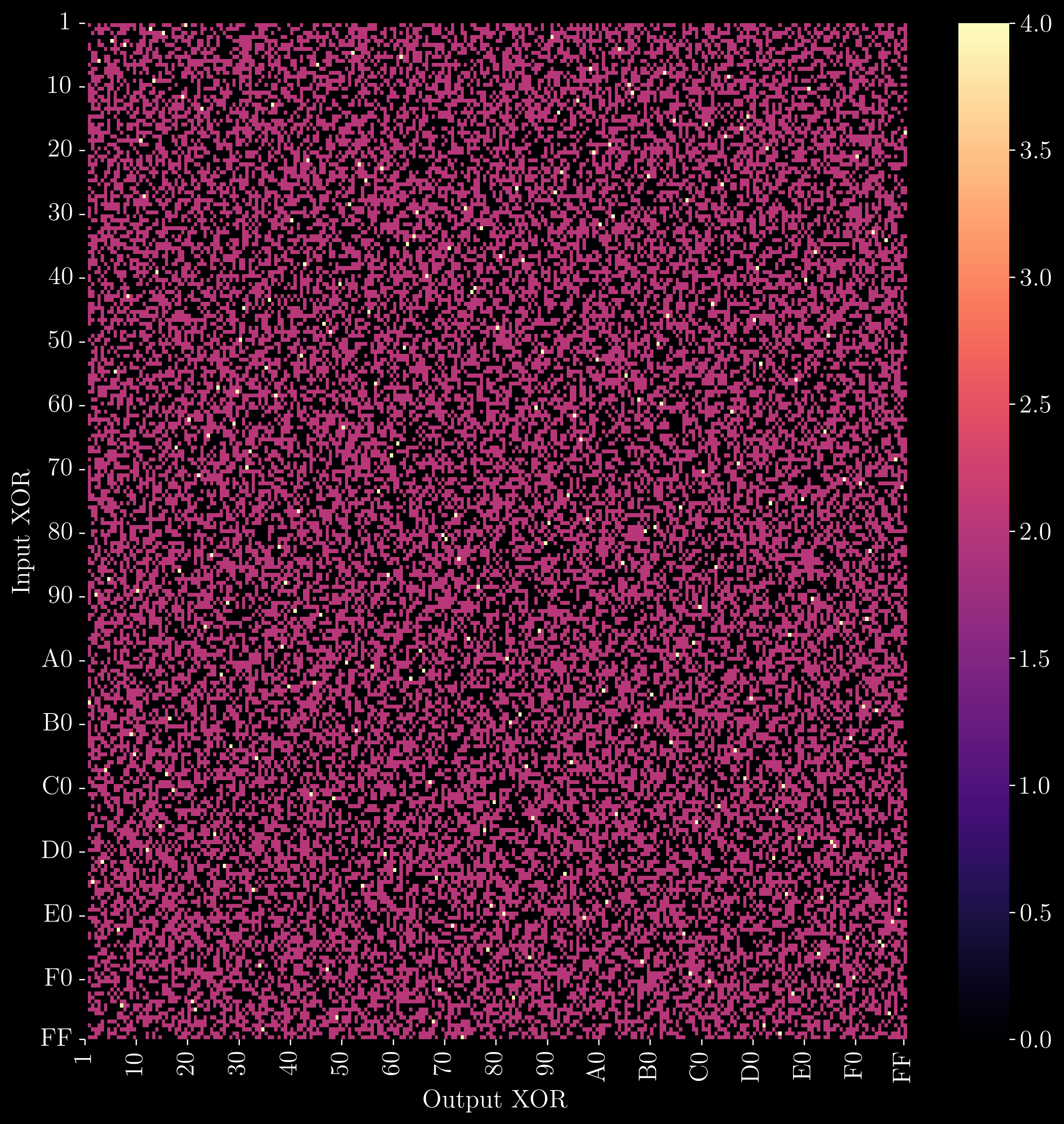
Success! The scale on the right shows that 4 is the highest count in the table. We have validated Nyberg’s claim.
There are still some hotspots on the AES DDT where the value is 4. Can we make the S-Box even more uniform, such that these hotspots are gone altogether? Well, Nyberg also showed that the multiplicative inverse mapping in GF(2^n) can result in a 2-uniform S-Box, but only if n is odd.
In AES, the field used is GF(2^8), and 8 is even… So why didn’t they just choose an odd number? Using 8 bits in their algorithm is much more practical, as computers are optimized for manipulating 8-bit bytes of memory. The authors of AES were willing to make this tradeoff, and time has told that it was a good decision, as AES is both incredibly efficient, and still has a good resistance to DC.
DC is a brilliant method that is still at the forefront of cryptographers’ minds during the design process of new encryption schemes. Thankfully, we have some mathematical safeguards that help to prevent it.
I hope you gained an understanding of DC and an insight into the beauty of cryptography. If you enjoyed this, you may also enjoy our previous post on Shamir’s Secret Sharing!
If you want to protect your users’ data using AES, use Evervault encryption; it’s the easiest way!
Implementing card tokenization in 2025 is straightforward and versatile. It also remains a crucial step to enhance payment security and streamline compliance efforts.
John Hetherton
Complete guide to implementing encryption for PCI Compliance in 2025. Understand must-haves and some practical strategies to maintain compliance.
John Hetherton