Shamir's Secret Sharing: Explanation and Visualization

Cryptography schemes are often difficult to understand, but they are intuitive when explained in a suitable medium. In 1979, famed cryptographer Adi Shamir proposed a new method for sharing secrets: Shamir’s Secret Sharing. Visualization works well for Shamir's scheme, which Evervault engineer David Nugent will show in this post.

What Is Shamir’s Secret Sharing Scheme?

Shamir’s Secret Sharing scheme is a cryptographic algorithm untrusted networks can use to distribute private information (also known as “secrets”) securely. Keyless security techniques (biometric data, private keys, etc.) use Shamir’s Secret Sharing to keep personal data safe and secure.

Why Is Shamir’s Secret Sharing Important?

Shamir’s Secret Sharing algorithm is flexible. Secret owners can add, edit, or remove shares whenever they’d like without messing with the original secret. You must meet the minimum threshold number of shares when reconstructing secrets—anything less, and the secret cannot be reconstructed. This protects your data from malicious attackers with limitless computational power.

Shamir’s Secret Sharing Visualization

Polynomial Depiction

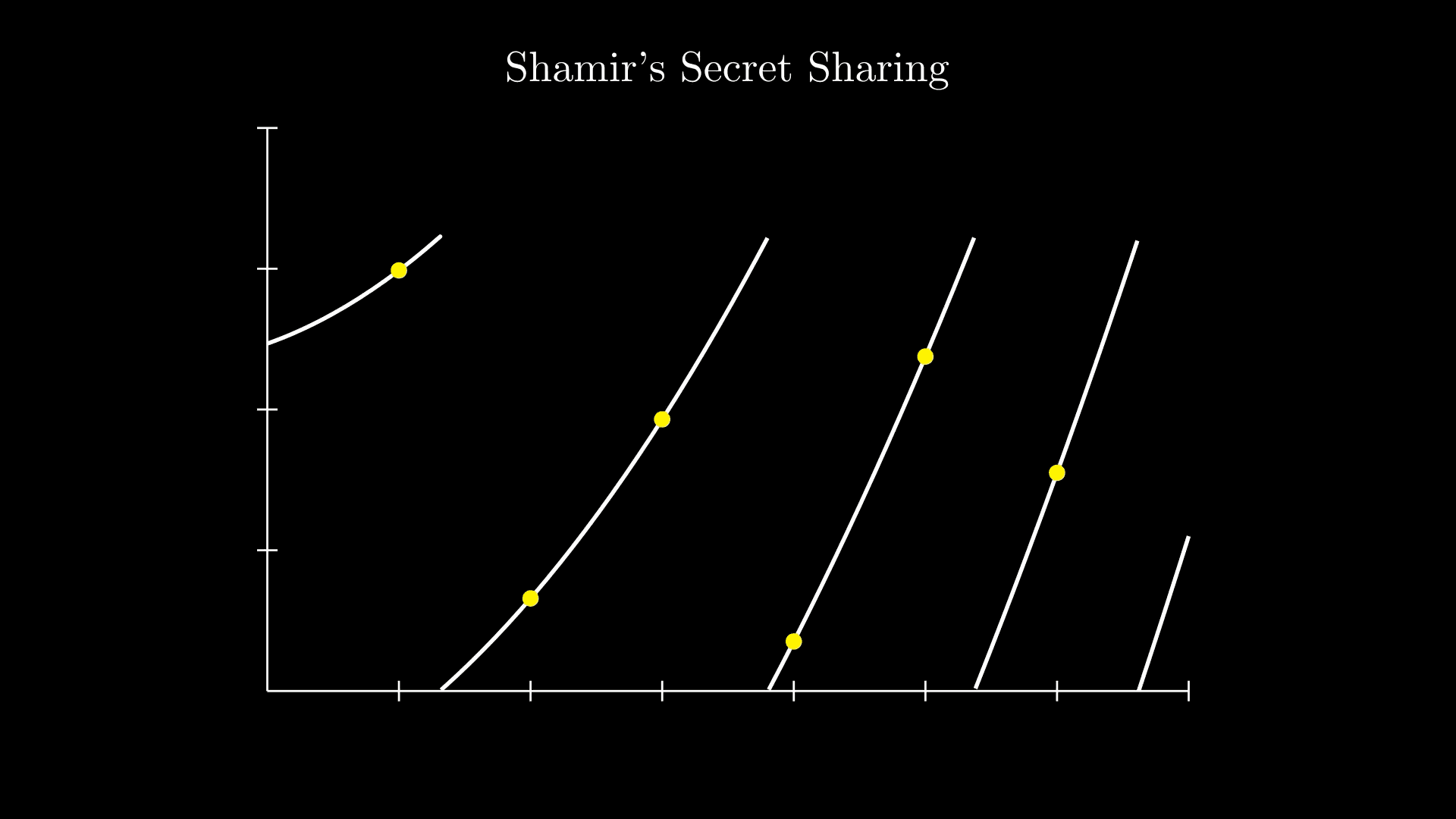
The first video clip depicts a polynomial. It is a degree 3 polynomial, as the largest power of x is 3. Polynomials work for secret sharing because you can give people some of the points on the curve without revealing to them what the polynomial is. This means you can share points, but someone can only find the polynomial if they have enough points. You need N+1 points to uncover a polynomial of degree N. These points are the 'shares' of our secret.

Polynomial Demonstration

As a demonstration, let's share the secret 1234. We’ll set the threshold as 3, i.e. you need at least three of the shares to find out the secret. Thus, we require the polynomial to be of degree 2. We need to pick two random numbers to be our coefficients. Let’s choose 94 and 166, which gives us the polynomial: 94x^2 + 166x + 1234. Here's what it looks like:

To get our shares, we need to find points on the polynomial. Although our threshold is 3, we can create any number of shares. You can share with as many people as you like, but someone needs to have 3 to reveal our secret. Let's, for example, create 6 shares by picking 6 points.

If we have 3 of these shares, we can interpolate them to find the polynomial and thus find our secret. Interpolation is essentially just finding the curve that passes through our points.

Security Flaws With Regular Polynomials

However, using regular polynomials has a security flaw. If you have some points but haven't enough to satisfy the threshold, you can use algebra to reduce the number of possible polynomials. This makes it easier to perform a brute-force attack to find the secret. In the example below, two points are stolen, and the attacker can try each possible polynomial (149 in this case) until they find the secret.

In an effective secret-sharing protocol, having less than the threshold number of shares should not give you any information about the secret. Therefore, using regular polynomials will not fit the bill.

Cyclic Polynomial

However, we can make a simple change to our polynomial to eliminate the above exploit: we turn it into a cyclic polynomial by applying a modulus. Another for the rusty: a modulus is basically just getting the remainder, e.g.

Applying a modulus makes a function cyclic, as it can only ever reach the number of the modulus, and then it will go back to zero again. Here’s what our function looks like when we apply a modulus of 1613.

We need to ensure our modulus is a prime number larger than our secret, our coefficients, and the number of shares we intend to generate.

The larger the prime chosen, the lower the probability of finding the secret. In this case, we'll select a relatively small one, 1613, as it works well with our visualization. Notice how unrelated the shares (points) look now:

We can still interpolate to find our secret when we have the threshold number of shares. But now, having less than the threshold does not give us more information about the secret than if we had no shares.

This scheme works for strings too! As strings are stored as binary, we can convert the binary representation of the string to decimal and use that representation as our secret.

Encrypt With Confidence

We've based this blog post on a great example from the Shamir's Secret Sharing Wikipedia page. You can check out the original paper to learn more about the scheme! Now that you understand how to share a secret, learn how to encrypt a string in less than five minutes with Evervault Inbound Relay.