Deep dive on fully homomorphic encryption: what is it and what makes it different?

Encryption is a cybersecurity technique that safeguards sensitive data from unauthorized access; it is utilized across various domains like online banking, healthcare, e-commerce, and secure communication.

In this article, we are going to be covering an important encryption technique known as Fully Homomorphic Encryption.

Definition and Explanation of Fully Homomorphic Encryption

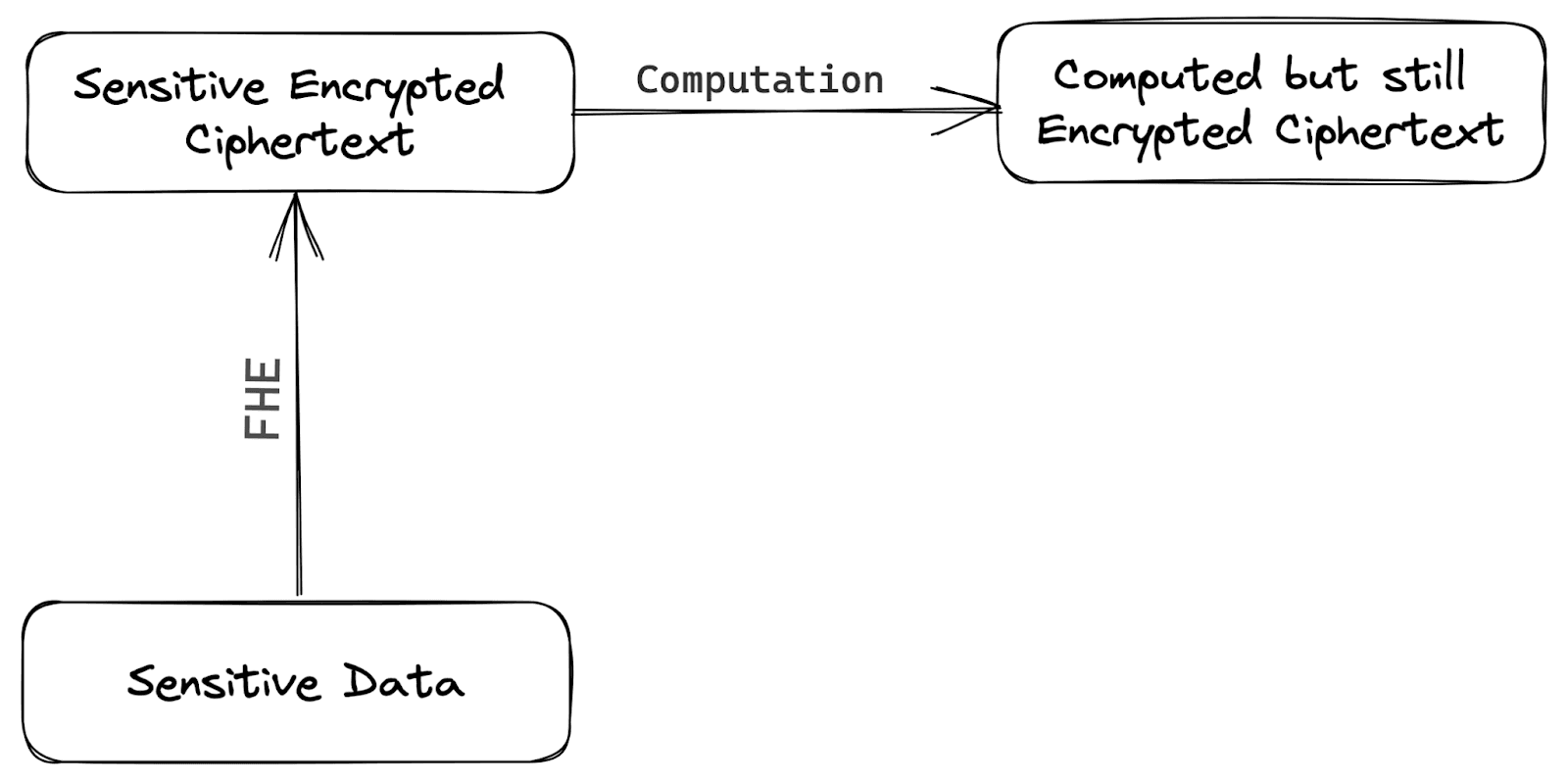
Fully Homomorphic Encryption (FHE) is a secure encryption method that enables computations to be executed on encrypted data without decrypting it. In simple terms, FHE allows for secure computations on encrypted data without exposing the original text (plaintext). This makes FHE a powerful tool for protecting sensitive data by allowing secure computation without the risk of data leaks, unauthorized access, or unwanted authorization.

FHE, or Fully Homomorphic Encryption, has the profound potential to greatly enhance our ability to handle sensitive data securely. This cutting-edge technology enables secure computation in scenarios that cannot be achieved using traditional encryption techniques.

Historical Background of Fully Homomorphic Encryption

The concept of homomorphic encryption was first introduced by Rivest, Adleman, and Dertouzos in their paper "On Data Banks and Privacy Homomorphisms'' published in 1978, but it was not until 2009 that the first practical implementation of FHE was developed by Craig Gentry. Gentry's implementation of FHE was based on lattice-based cryptography and allowed basic arithmetic operations to be performed on encrypted data.

Since then, more significant progress in improving the efficiency and practicality of FHE.

Types of Homomorphic Encryption Schemes

There are several types of homomorphic encryption schemes, each with its strengths and weaknesses. In this section, we are going to discuss briefly some of the most common types of homomorphic encryption schemes:

Partially Homomorphic Encryption (PHE): This is the easiest type of homomorphic encryption. It enables computations on encrypted data of a single type, like addition or multiplication. However, it can't handle computations of different types in a single operation, which makes it less powerful than fully homomorphic encryption. Nonetheless, it is more efficient.

Somewhat Homomorphic Encryption (SHE): This type of homomorphic encryption allows for computations on encrypted data of different types, but only to a certain degree. It has limitations on the number of computations that can be performed before the accuracy of the computation begins to degrade. It is more powerful than PHE but still less powerful than fully homomorphic encryption.

Fully Homomorphic Encryption (FHE): This is the most powerful type of homomorphic encryption, allowing for arbitrary computations on encrypted data of any type. It is also the most computationally expensive and difficult to implement, which has been a major challenge for folks trying to use it in the real world.

Each type of homomorphic encryption has its trade-offs between computational efficiency and functionality, which makes it important to choose the appropriate type based on the specific use case.

In the next section of this article, we will dive deeper into how Fully Homomorphic Encryption works and its principles.

Principles of Fully Homomorphic Encryption (FHE)

Fully homomorphic encryption (FHE) enables direct computation on ciphertexts, rather than the original plaintexts, using advanced mathematical techniques. This is made possible through two primary operations - encryption and evaluation.

Encryption: Encryption is the process of converting understandable and meaningful plain data into scrambled and incomprehensible ciphertext with the help of an encryption key. In fully homomorphic encryption (FHE), the plaintext data is converted into a specific kind of ciphertext with additional information that enables computations to occur directly on the ciphertext, without requiring decryption. This is different from the traditional ciphertext, enabling encryption to happen with added convenience.

Evaluation: Evaluation refers to the process of performing computational tasks on encrypted data without exposing the original data. In Fully Homomorphic Encryption (FHE), this is attained by utilizing specific mathematical functions that can operate directly on fully homomorphic ciphertexts. These functions are specifically designed to maintain the authenticity of the original data, even when calculations are made on the encrypted data.

The Mathematics of Fully Homomorphic Encryption (FHE)

One of the key mathematical techniques used in FHE is the concept of "multilinear maps." Multilinear maps are a type of mathematical function that can operate on multiple variables simultaneously while preserving certain algebraic properties. These properties are essential for ensuring the security and integrity of the data being processed.

Another important mathematical concept used in FHE is "bootstrapping." Bootstrapping is a process that allows a fully homomorphic ciphertext to be "re-encrypted" into a new fully homomorphic ciphertext that can be used to perform additional computations. This is important because FHE computations can quickly become complex and unwieldy, and bootstrapping allows for the computation on the encrypted ciphertext to be simplified and streamlined.

The mathematical basis of FHE can involve sophisticated and advanced concepts in abstract algebra, number theory, and cryptography. However, the basic idea behind FHE is relatively simple: by allowing computations to be performed directly on ciphertexts, FHE enables secure and private processing of sensitive data without ever revealing the original plaintext.

Performance and Efficiency of Fully Homomorphic Encryption (FHE)

Performance and efficiency are two crucial aspects of any encryption scheme, and fully homomorphic encryption is no exception. In this section we will discuss the performance and efficiency of fully homomorphic encryption.

The performance and efficiency of FHE are determined by various factors, including the encryption and decryption times, ciphertext size, and the number and complexity of the operations performed on the ciphertext.

One of the most significant challenges in FHE is bootstrapping. Bootstrapping is an important process in FHE that allows the ciphertext to be refreshed without revealing its plaintext content. It is necessary for performing complex computations on the ciphertext. However, bootstrapping is a computationally expensive operation that can significantly impact the performance of FHE.

There have been various techniques to optimize bootstrapping and improve the performance of FHE. One of the most promising approaches to this is known as the “Gentry-Szydlo technique”. This provides an optimized method of bootstrapping that significantly reduces the computational overhead involved in the process. This technique has been shown to improve the performance of FHE in a very significant manner.

Efficiency is another critical aspect of FHE. The encrypted ciphertext size of FHE is typically much larger than the plaintext size, which can impact its efficiency. Compression techniques can be used to reduce the size of the ciphertext, thereby improving the efficiency of FHE.

In conclusion, the performance and efficiency of fully homomorphic encryption are important to consider while thinking of its practical application.

Comparison with other encryption schemes

The major comparison point for FHE and other encryption schemes is the process through which data is encrypted. FHE allows for computation on encrypted data without the need to convert the data to plain text while other encryption schemes typically require the decryption of data before any form of computation can be performed. This means that FHE allows for more secure and private computation, as sensitive data can remain encrypted throughout the computation process.

Another key difference between FHE and other encryption schemes is the level of complexity involved in the encryption and decryption processes. FHE encryption can be more complex than other methods, as it involves adding noise to the encrypted data to protect against attacks. This added complexity can result in increased security for the data, as the added noise makes it more complex for attackers to decipher the encrypted data.

Advantages and Disadvantages of Fully Homomorphic Encryption

FHE can be advantageous in various situations but it equally has its disadvantages. In this section, we are going to cover some of the advantages and disadvantages of FHE.

Advantages

• FHE provides better security for sensitive data compared to other encryption schemes because the encrypted data does not need to be converted to plain text before computations can happen.
• It is resistant to attacks from hackers as it takes a lot of effort to decrypt encrypted with FHE.
• The encrypted data stays encrypted at all times irrespective of what processes need to happen on the data.

Disadvantages

• FHE requires a lot of computational resources for its encryption process.
• It can be complex and difficult to understand and implement compared to other encryption schemes.
• It is slow by default and would need several adjustments to improve its performance.
• It is not yet ready to be used for high-scale and general-purpose use cases.

Real-world applications

While FHE is not yet ready to be used for high-scale and general-purpose use cases, it can still be used in the real world in several industries.

A very practical use case of FHE in the real world is in the healthcare sector. We all know how confidential and sensitive patients' data in a hospital are. Consider a scenario where a medical research scientist needs real-world data to carry out experiments like identifying potential health risks, clinical trials or even discovering new treatments. They reach out to a hospital for this data but the management of the hospital is very sceptical about exposing their patients' data to a non-member of their staff. With FHE, patients' data can be encrypted and secure computations on this sensitive medical data can be performed without compromising the privacy of patients.

Another real-world use case of FHE in the real world is in the Financial services sector. We all know how sensitive financial data is, in cases where computation like calculating credit scores, investments and the like is needed, FHE can be used to encrypt the sensitive financial data and the computation can still happen on the encrypted data without the need to decrypt it. This makes user data private and safe from all forms of attacks and unauthorized access.

In the communications industry, FHE can be used to build platforms that allow 100% secure communication. Secure communication can include secure emails, secure messaging and secure file sharing. With FHE in place, computations on encrypted messages can be carried out without the need for decryption.

Fully Homomorphic Encryption when gotten right has numerous benefits to the real world. It can really improve the security of our data in the real world and allow companies to build hack-proof products for their users.

Conclusion

In conclusion, Fully homomorphic encryption is a unique and powerful encryption scheme that provides several advantages over other encryption schemes. Although it has some disadvantages that come with using it and these disadvantages make it look quite unrealistic or let’s say ahead of its time, there are already some real-world applications in today’s world for the technology. In industries where data privacy and security are essential, FHE can play a part in improving the privacy and security of data. As the technology continues to evolve and become more widely used and understood, we can expect to see even more innovative applications of FHE in the years to come.

Further Reading:

How we built the Evervault Encryption Engine (E3)